NOMBRES COMPLEXES

Les nombres complexes ont révolutionné les mathématiques en élargissant l’ensemble des nombres réels pour inclure des solutions aux équations impossibles dans ce domaine. Ils ont été introduits pour résoudre des équations du type 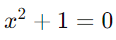et ont depuis trouvé des applications étendues dans de nombreux domaines.

1. Définition et Propriétés des Nombres Complexes
Les nombres complexes sont des nombres de la forme a+bi, où a et b sont des nombres réels et i est l’unité imaginaire définie comme la racine carrée de −1. L’ensemble des nombres complexes est noté C et possède des propriétés uniques, telles que la notion de partie réelle et imaginaire, les opérations arithmétiques, les formes polaires, etc.

2. Applications des Nombres Complexes
Les nombres complexes ont des applications dans divers domaines professionnels :

Ingénierie et Physique : En ingénierie, les nombres complexes sont utilisés dans l’analyse de circuits électriques, la résolution de problèmes liés aux ondes et aux signaux. En physique, ils interviennent dans la description de phénomènes tels que les oscillations, les ondes électromagnétiques, etc.

Mathématiques et Sciences : En mathématiques, les nombres complexes sont utilisés dans l’analyse complexe, la théorie des équations différentielles, la géométrie, et d’autres domaines. En sciences, ils sont utilisés pour modéliser des phénomènes non réels et abstraits.

Technologie et Informatique : Dans le domaine de l’informatique, les nombres complexes sont utilisés dans le traitement du signal, la compression d’images, la conception de jeux vidéo, et dans des algorithmes de cryptographie.

Finance et Économie : En finance, ils peuvent intervenir dans la modélisation de comportements non linéaires et dans l’évaluation de certains produits dérivés.

Les nombres complexes constituent un outil puissant pour modéliser des phénomènes abstraits et non réels, permettant des analyses approfondies et des solutions à des problèmes qui étaient auparavant considérés comme insolubles dans le domaine des nombres réels.